Nella lezione precedente abbiamo introdotto il metodo delle tensioni di nodo. Vediamo ora alcuni esempi che meglio illustrano l'approccio.
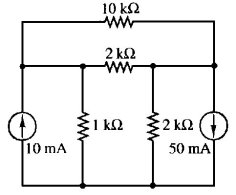
Vogliamo risolvere il circuito di figura 3.4 ricavando le correnti e le tensioni incognite. Come si vede dalla figura 3.5, i nodi sono in tutto tre (lo si verifica facilmente facendo tendere a lunghezza zero i pezzi di ramo non essenziali). Assunto il nodo 3 come nodo di riferimento e posto il suo potenziale pari a zero, assegnati i versi (arbitrari) delle correnti, applichiamo la legge di Kirchhoff delle correnti al nodo 1:
 |
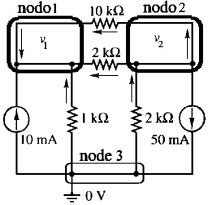 |
| Figura 3.4 | Figura 3.5 |
0.01 + (0 - v1) / 1000 + (v2 - v1) / 10000 + (v2 - v1) / 2000 = 0
mentre al nodo 2 si ha:
(0 - v1) / 2000 = (v2 - v1) / 10000 + (v2 - v1) / 2000 + 0.05
Si noti come ciascuna corrente sia stata espressa direttamente in funzione delle tensioni di nodo (la scrittura delle equazioni di nodo è nient'altro che una semplice applicazione della legge di Ohm e della legge di Kirchhoff delle correnti). Riordinando i termini e ponendo in sistema le equazioni, si ha:
 |
(1 /1000 + 1 / 10000 + 1/2000)v1 + (-1/10000 - 1/2000)v2 = 0.01 |
| (-1/10000 - 1/2000)v1 + (1 /1000 + 1 / 10000 + 1/2000)v2 = -0.05 |
Con facili calcoli, si giunge al seguente sistema lineare:
 |
1.6v1 -0.6v2 = 0.01 |
| -0.6v1 + 1.1v2 = -0.05 |
Risolvendo, si ricava v1 = -13,37 V e v2 = -52,86 V. Noti i potenziali di nodo, possiamo determinare le tensioni e le correnti di ramo nel circuito. Per esempio, la corrente che attraversa il resistore da 10 kΩ è data da:
i10kΩ = (v2 - v1) / 10000 = -3.93 mA
Il segno negativo sta ad indicare che il verso da noi (arbitrariamente) scelto per la corrente attraversante tale resistore è contrario a quello effettivo (cioè, la corrente va in realtà dal nodo 1 al nodo 2). Come ulteriore esempio, si consideri la corrente attraverso il resistore da 1 kΩ:
i1kΩ = (0 - v1) / 1000 = 13.57 mA
In questo caso la corrente è positiva, e pertanto il verso della corrente da noi prescelto è esatto. Si può continuare l'analisi ramo per ramo, iniziata in questo esempio, onde verificare che la soluzione ottenuta è effettivamente corretta.
Ricavare le tensioni di nodo per il circuito di figura 3.6. Si assumano i seguenti dati:
R1 = 1 kΩ, R2 = 500 kΩ, R3 = 2.2 kΩ, R4 = 4.7 kΩ, ia = 1 mA, ib = 1 mA

Figura 3.6
Soluzione:
Per scrivere le equazioni al nodo, prima di tutto osserviamo (figura 3.7) che qui abbiamo tre nodi: a, b e c.
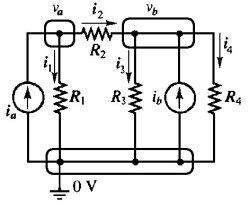
Figura 3.7
Scegliamo il nodo c come nodo si riferimento, a cui assegniamo potenziale nullo. Applichiamo ora la legge di Kirchhoff delle correnti ai nodi a e b; per il nodo a si ottiene:
ia = (va - 0) / R1 + (va - vb) / R2
Per il nodo b si ha:
(va - vb) / R2 = (vb - 0) / R3 + (vb - 0) / R4
Riordinando i termini e ponendo in sistema le due equazioni, si ha:
 |
(1 / R1 + 1 / R2)va + (- 1 / R2)vb = ia |
| (- 1 / R2)va + (1 / R2 + 1 / R3 + 1 / R4)vb = ib |
Sostituendo i valori numerici in queste equazioni, si ottiene:
 |
3va + 2vb = 1 |
| -2va + 2.67vb = 2 |
La soluzione, va = 1.667 V, vb = 2 V può essere ottenuta risolvendo il sistema di equazioni.
Il metodo delle tensioni di nodo è il metodo più generale per l'analisi dei circuiti elettrici. In questo paragrafo illustreremo la sua applicazione ai circuiti lineari a resistenza. Il metodo consiste nel definire il potenziale (ovvero la tensione) a ciascun nodo come una variabile indipendente.
Poiché il potenziale ha senso solo se riferito ad un potenziale di riferimento, anziché prendere il potenziale terrestre, uno dei nodi viene assunto come nodo di riferimento ed il suo potenziale diviene il potenziale di riferimento (cioè lo zero del potenziale); il potenziale di ogni altro nodo viene quindi espresso in funzione di questo riferimento.
Una volta definiti i potenziali di nodo, si può applicare la legge di Ohm tra due nodi adiacenti, in modo da determinare la corrente che transita in ogni ramo. Nel metodo delle tensioni di nodo, ogni corrente di ramo viene espressa in funzione di uno o più potenziali di nodo; in questo modo, le correnti non compaiono esplicitamente nelle equazioni.
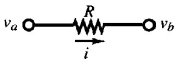
Figura 3.1 Notazione della corrente di ramo nell'analisi per nodi
Consideriamo la figura 3.1: come si definisce la corrente di ramo in questo metodo? Noi assegniamo i potenziali ai nodi va e vb; la corrente di ramo che transita da a a b è allora espressa in funzione di questi potenziali di nodo:
i = (va - vb) / R
Una volta definite tutte le correnti di ramo in funzione delle tensioni ai nodi, si applica la legge di Kirchhoff delle correnti ad ogni nodo, prendendo le correnti entranti nei nodi con il segno positivo e quelle uscenti con il segno negativo (ma è anche possibile scegliere la convenzione opposta; è bene, tuttavia, adoperare sempre la stessa convenzione per evitare di fare confusione): in tal modo deve essere Σik = 0, dove k è l'indice dei rami collegati al nodo. Alla luce delle convenzioni di segno adottate per le correnti ai nodi, possiamo anche scrivere che:
Σiin = Σiout (F3.1)
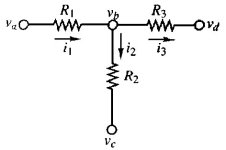
Figura 3.2 Uso della legge di Kirchhoff nell'analisi ai nodi
cioè, la somma delle correnti che entrano nel nodo deve eguagliare la somma delle correnti che escono dallo stesso. La figura 3.2 illustra questa procedura: in base alla legge di Kirchhoff si ha, perciò:
i1 - i2 - i3 = 0 ovvero i1 = i2 + i3
Nel metodo delle tensioni ai nodi si scrive, quindi:
(va - vb) / R1 = ((vb - vc) / R2) + ((vb - vd) / R3)
L'applicazione sistematica di questo metodo ad un circuito con n nodi porta a scrivere n equazioni.
Tuttavia, una delle tensioni di nodo è il potenziale di riferimento ed è perciò già noto, giacché è di solito convenientemente posto pari a zero. Così, possiamo scrivere n-1 equazioni indipendenti in n-1 variabili indipendenti (costituite dalle tensioni di nodo). L'analisi ai nodi fornisce il minimo numero di equazioni necessarie per risolvere il circuito, in quanto ogni tensione o corrente di ramo può essere determinata dalla conoscenza delle tensioni di nodo.
Il metodo dell'analisi per nodi può essere definito come una sequenza di passi come segue:
Seguendo la procedura appena esposta, si ha la garanzia di trovare la soluzione corretta di un dato circuito, una volta che si siano identificati propriamente i nodi e che la legge di Kirchhoff delle correnti sia stata applicata consistentemente. Per illustrare il metodo, consideriamo il circuito di figura 3.3. Il circuito è mostrato in due forme diverse per illustrare rappresentazioni grafiche equivalenti dello stesso circuito.
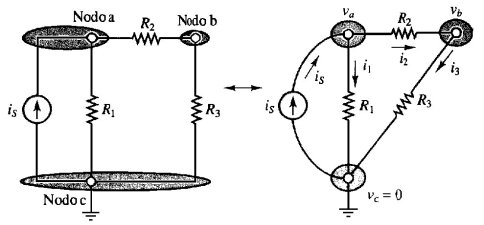
Figura 3.3
Il circuito sulla destra non lascia dubbi su dove siano i nodi; infatti, non ci si deve far ingannare dal disegno, in cui i rami né attivi né passivi, ma di puro collegamento, sembrano generare più nodi: è consigliabile, in effetti, ridisegnare a parte il circuito (come fatto qui) eliminando tutti i pezzi di ramo di puro collegamento (facendoli tendere idealmente a lunghezza zero): in tal modo resterà solo ciò che è effettivamente indispensabile, come fatto in figura 3.3.
La direzione delle correnti viene scelta arbitrariamente (assumiamo, così, che iS sia una corrente positiva). L'applicazione della legge di Kirchhoff delle correnti (formula 3.1) al nodo a consente di scrivere:
iS = i2 + i1 (F3.2)
mentre al nodo b si ha:
i2 = i1 (F3.3)
E' istruttivo verificare (almeno la prima volta che si applica il metodo) che non è necessario applicare la legge di Kirchhoff delle correnti al nodo di riferimento. L'equazione che si ottiene al nodo c è infatti:
iS = i1 + i3 (F3.4)
che è una equazione dipendente dalla 3.2 e dalla 3.3; infatti può essere ottenuta per somma membro a membro tra la 3.2 e la 3.3 (lo si verifichi per esercizio). Questa osservazione conferma l'affermazione fatta in precedenza: in un circuito contenete n nodi, possiamo scrivere al massimo n-1 equazioni indipendenti. Ora, nell'applicare il metodo delle tensioni di nodo, le correnti i1, i2, ed i3 sono espresse come funzioni di va, vb e vc, che sono le variabili indipendenti. La legge di Ohm richiede che i1, per esempio, sia dato da:
i1 = (va - vc) / R1 (F3.5)
poiché la differenza di potenziale, va - vc, ai capi di R1, provoca il passaggio della corrente i1 dal nodo a al nodo c. Analogamente:
i2 = (va - vb) / R2 (F3.6a)
i3 = (vb - vc) / R3 (F3.6a)
Sostituendo queste tre espressioni nella 3.2 e nella 3.3, otteniamo le seguenti relazioni:
 |
iS = va / R1 + (va - vb) / R2 (F3.7) |
| (va - vb) / R2 = vb / R3 (F3.8) |
Le equazioni 3.7 e 3.8 possono anche essere ricavate direttamente dal circuito con un po' di pratica (lo vedremo). Si noti che queste equazioni possono essere risolte per va e vb, assumendo che iS, R1, R2 e R3 siano noti. Lo stesso sistema può essere riscritto come segue:
 |
(1 / R1 + 1 / R2)va + (- 1 / R2)vb = iS (F3.9a) |
| (- 1 / R2)va + (1 / R2 + 1 / R3)vb = 0 (F3.9b) |
Nella prossima lezione vedremo degli esempi che illustrano ulteriormente l'applicazione del metodo.
Nella risoluzione di reti complesse di circuiti elettrici può essere opportuno, o necessario, ricorrere alla sostituzione (parziale e successiva) di triangoli di resistenze (figura 2.55) in stelle di resistenze (figura 2.56), o viceversa:
|
|
|
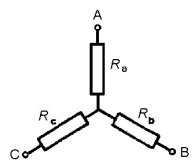 Figura 2.56 Stella di resistenze |
o viceversa, sostituzioni possibili a mezzo delle seguenti relazioni: per passare dal triangolo alla stella:
Ra = RabRca / (Rab + Rbc + Rca) (F2.33)
Rb = RbcRab / (Rab + Rbc + Rca) (F2.34)
Rc = RcaRab / (Rab + Rbc + Rca) (F2.35)
Per passare invece da una stella ad un triangolo:
Rab = RaRb × (1/Ra + 1/Rb + 1/Rc) (F2.33)
Rbc = RbRc × (1/Ra + 1/Rb + 1/Rc) (F2.33)
Rca = RaRc × (1/Ra + 1/Rb + 1/Rc) (F2.33)
Ci si può chiedere se l'equivalenza della sostituzione sia vera: proviamo a vederlo in un caso: consideriamo il morsetto C scollegato da qualsiasi sistema (facciamo finta, cioè, che non ci sia). Se ho il triangolo, tra i morsetti A e B devo perciò avere:
RAB = Rab || (Rca + Rbc) (F2.39)
Se invece ho la stella, la resistenza totale tra i morsetti A e B sarà:
RAB = Ra + Rb) (F2.40)
Con rapidi calcoli di sostituzione, partendo dalla F2.39, ed usando la formula F2.21 per i resistori in parallelo (Cfr. Lezione 2.8), e la 2.36, 2.37 e 2.38 si può dimostrare (e la dimostrazione è lasciata per esercizio) che si arriva esattamente alla formula 2.40.
Si può giungere ad un analogo risultato prendendo anche le altre due coppie di morsetti; alternativamente, è possibile partire dalla 2.40 e mostrare che tramite le 2.33, 2.34 e 2.35 si giunge proprio alla 2.39. Infine, il lettore può, per esercizio, creare altri "casi" per testare la validità dell'equivalenza triangolo-stella.
Quando si approccia un circuito elettrico per analizzarlo, la prima osservazione da fare è che le variabili rilevanti nell'analisi delle reti sono le tensioni di nodo e le correnti di ramo. Ciò non è altro che la conseguenza della legge di Ohm. Si consideri il ramo di figura 2.49, costituito da un singolo resistore. In questo caso, una volta che è stata definita la tensione vR ai capi del resistore R, la corrente iR passerà attraverso il resistore secondo la legge vR = iRR. Ma la tensione vR, che provoca il passaggio della corrente, è in realtà la differenza di potenziale elettrico tra i nodi a e b:
vR = va - vb (F2.31)
Quale significato assegniamo alle variabili va e vb? Non abbiamo forse affermato in precedenza che la tensione è una differenza di potenziale? Risulta allora legittimo definire la tensione in un singolo punto (nodo) di un circuito?
Ogni volta che ci riferiamo alla tensione di un nodo in un circuito, noi facciamo l'implicita assunzione che la tensione in quel nodo è la differenza di potenziale tra il nodo stesso ed un nodo di riferimento chiamato terra, che è collocato in qualche altra parte del circuito ed a cui viene assegnato per comodità il potenziale di zero volt.
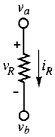
Figura 2.49
Così, l'espressione 2.31 significa che vR è la differenza tra le differenze di tensione va - vc e vb - vc , dove vc è il potenziale (arbitrario) della terra. Si noti che l'equazione 2.31 vale anche nel caso in cui al nodo c di riferimento non sia assegnato un potenziale di zero volts, in quanto:
vR = va - vb = (va - vc) - (vba - vc) (F2.32)
Cos'è allora la terra? La scelta della parola terra non è arbitraria. Questo punto può essere illustrato tramite una semplice analogia con la fisica del moto dei fluidi.
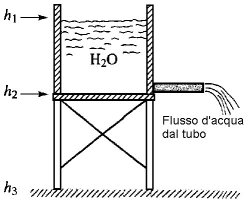
Consideriamo un serbatoio d'acqua, come mostrato in figura 2.50, collocato ad una certa altezza sopra il livello del terreno. L'energia potenziale dovuta alla gravità permette all'acqua di uscire dal tubo con una certa portata. La pressione che fa uscire l'acqua dal tubo è direttamente correlata alla differenza di livello h2 - h1 in modo tale che la pressione è nulla quando h2 = h1. Ora, il punto h3, corrispondente al livello del terreno, lo si definisce a potenziale zero. Si vede facilmente che la pressione che agisce sul fluido nel tubo è realmente provocata dalla differenza di energia potenziale, (h1 - h3) - (h2 - h3). Si può vedere, allora, che non è necessario assegnare un preciso livello di energia al livello h3; in effetti, sarebbe molto sciocco farlo, giacché ciò che conta nei problemi di questo tipo è la differenza di energia potenziale (o potenziale relativo), e non il potenziale assoluto.
 superficie terrestre |
 |
| Figura 2.50 Analogia idrostatica | |
In modo analogo, in ogni circuito si può definire un punto come terra e gli si assegna per comodità il potenziale elettrico pari a zero volt. Si noti che, a meno che non le si colleghino di proposito insieme, le terre in due circuiti completamente separati non sono necessariamente allo stesso potenziale. Questa affermazione può sembrare oscura, ma l'esempio successivo dovrebbe chiarire il concetto.
Le automobili ed i veicoli commerciali sono equipaggiati con una batteria acido-piombo (di solito a 12 V) per fornire energia elettrica ad una certa gamma di accessori. I circuiti elettrici all'interno del veicolo sono tutti collegati ad una terra comune, che, per comodità, non è altro che la scocca metallica dell'automezzo (vedi figura 2.52). Questo tipo di connessione a terra è in inglese detta chassis ground (letteralmente "terra alla scocca", in italiano "messa a terra a massa").
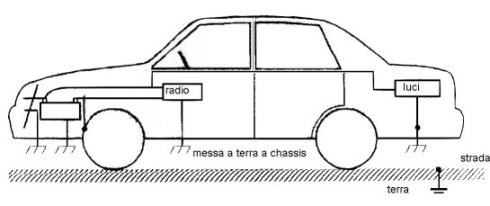
Figura 2.52 Esempio di messa a terra a massa
Si noti che l'automezzo viaggia su di un supporto isolante, ossia i suoi pneumatici. Di conseguenza, il potenziale di terra della scocca non è necessariamente lo stesso del potenziale di terra della Terra. Quest'ultima quantità è infatti indicata in inglese col termine earth ground (letteralmente "terra alla Terra", la messa a terra propriamente detta, figura 2.53).
 a) |
 b) |
| Figura 2.51 a) messa a terra; b) messa a terra a massa | |
Spesso i due tipi di terra coincidono. Per esempio, una lavatrice la cui circuiteria interna è collegata all'involucro metallico (châssis/scocca o "massa") è anche messa a terra rispetto alla Terra (figura 2.53).
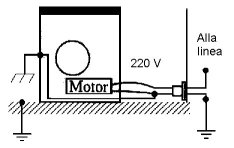
Figura 2.53 Messa a terra
Questa è una buona idea dal punto di vista della sicurezza. Se le due terre non coincidessero, si potrebbe generare una differenza di potenziale tra la Terra e lo châssis/scocca, e l'inconsapevole utilizzatore potrebbe correre il rischio di restare fulminato toccando la lavatrice che sta sulla superficie del terreno, chiudendo così il circuito tra lo châssis e la Terra. Noi, in seguito, non distingueremo tra i due tipi di terra (ed useremo il simbolo comune della terra), a meno che non sia richiesto dal problema specifico.
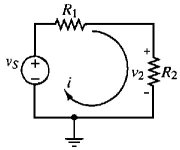
Vogliamo identificare tensioni di ramo e di nodo e correnti di loop e di maglia nel circuito di figura 2.54. Allo scopo, facciamo una tabella esplicativa: mediante un'analisi del circuito proposto, si possono identificare le seguenti tensioni:
| Tensioni di nodo | Tensioni di ramo |
| va = vS (tensione del generatore) | vS = va - vd = va |
| vb = vR2 | vR1 = va - vb |
| vc = vR4 | vR2 = vb - vd = vb |
| vd = 0 (terra) | vR3 = vb- vc |
| vR4 = vc - vd = vc | |
|
Le correnti ia , ib ed ic sono correnti di loop, ma solo ia e ib sono correnti di maglia. |
|
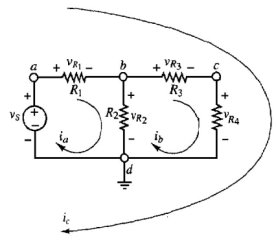
Figura 2.54
Nei paragrafi precedenti abbiamo analizzato gli elementi circuitali basilari: generatori, resistori e strumenti di misura. Abbiamo così raccolto tutti gli strumenti che ci consentono di definire una rete elettrica.
E' opportuno, a questo punto, definire formalmente i costituenti di un circuito elettrico; le definizioni che seguono sono una parte della terminologia standard dell'ingegneria elettrica ed elettronica.
Un ramo è una porzione di circuito connessa a due terminali (es.: due morsetti). Una ramo può essere costituito da uno o più elementi circuitali (figura 2.45). Nella pratica, ogni elemento circuitale connesso a due terminali è un ramo.
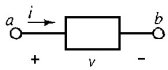 i = corrente di ramo v = tensione di ramo |
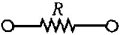 resistore ideale |
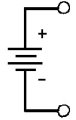 batteria |
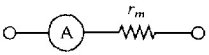 amperometro reale |
| Figura 2.45 Esempi di ramo | |
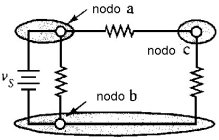
Un nodo è una giunzione tra due o più rami (si definisce spesso una giunzione tra due soli rami come nodo triviale). La figura 2.46 illustra il concetto. In effetti, ogni connessione che si ottiene saldando insieme vari terminali è un nodo. E' molto importante identificare i nodi appropriatamente nell'analisi delle reti elettriche, perchè dalla corretta identificazione vedremo che dipenderà l'analisi del circuito.
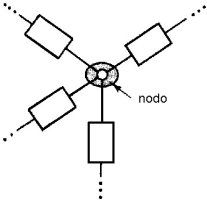 |
|
 |
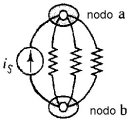 |
| Figura 2.46 Esempi di nodo | |
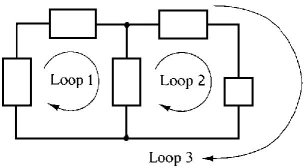
Per loop si intende qualsiasi connessione chiusa di rami che inizia ad un terminale di un ramo e finisce al terminale opposto dello stesso ramo. Le varie configurazioni di un loop sono illustrate in figura 2.47.
 |
|
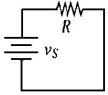 circuito a 1 loop |
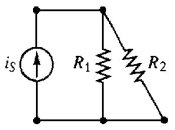 circuito a 3 loop |
| Figura 2.47 Esempi di loop | |
Si noti come due diversi loop nello stesso circuito possano includere elementi o rami uguali.
Una maglia è un loop che non contiene altri loop. Le maglie sono un concetto molto importante per certi metodi di analisi. Il circuito di figura 2.47 presenta tre loop, ma consiste di sole due maglie: il loop 1 ed il 2 sono maglie, mentre il loop 3 non è una maglia, perché racchiude in sé sia il loop 1 che il 2. Anche il circuito ad un solo loop di figura 2.48 è un circuito ad una sola maglia.
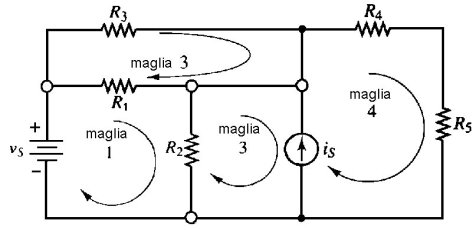
Figura 2.48 Esempio di analisi per maglie
Il circuito di figura 2.48, costituito da quattro maglie, ci consente di renderci conto di come sia più semplice visualizzare le maglie che non i loop. infatti, in questo caso i loop sono addirittura quattordici (la verifica è lasciata al lettore).
L'analisi di una rete elettrica consiste nel determinare ciascuna delle correnti di ramo e/o delle tensioni di nodo incognite: é pertanto importante definire le variabili importanti quanto più chiaramente possibile, in maniera sistematica. Una volta identificate le variabili note e le incognite, si costruisce un set di equazioni, che correlino queste variabili, che deve essere risolto per mezzo di tecniche appropriate.
L'analisi dei circuiti elettrici consiste nello scrivere il più piccolo set di equazioni sufficiente a ricavare la soluzione per tutte le variabili incognite. Le procedure per scrivere queste equazioni sono oggetto del Capitolo 3 e sono ben codificate in semplici regole. l'analisi dei circuiti elettrici è enormemente semplificata se si seguono delle convenzioni standard. Ci proponiamo nelle prossime lezioni il compito di fornire le procedure preliminari per rendere l'analisi di un circuito elettrico più... "digeribile".