Benché i circuiti elettrici possano assumere forme molto complicate, perfino i circuiti più complessi possono essere ridotti a combinazione di elementi circuitali in parallelo ed in serie.
Per questa ragione è importante divenire familiari con i circuiti in serie ed in parallelo quanto prima possibile, addirittura prima di accostarsi formalmente alla discussione dell'analisi delle reti.
I circuiti in serie ed in parallelo hanno un rapporto diretto con le leggi di Kirchhoff (cfr. Lezione 1 e Lezione 2 in questo capitolo). L'obiettivo di questa e della prossima lezione è di illustrare due comuni circuiti sulla combinazione di resistori in serie ed in parallelo: il partitore di tensione e quello di corrente. Questi circuiti costituiscono la base di tutta l'analisi delle reti: per questo risulta importante approfondire questo argomento.
Prima di addentrarci nella analisi circuitale, introduciamo due convenienti idealizzazioni dell'elemento resistenza che sono fornite dai casi limite della legge di Ohm in cui la resistenza di un elemento circuitale va a zero o all'infinito. Un elemento circuitale la cui resistenza si approssima a zero è chiamato un corto circuito.
Intuitivamente, ci si aspetta che un corto circuito consenta il passaggio senza impedimenti della corrente. In effetti, i conduttori metallici (come ad esempio i fili corti di grande diametro) approssimano il comportamento di un corto circuito.
Formalmente, un corto circuito è definito come un elemento circuitale che presenta ai suoi estremi una differenza di potenziale nulla, indipendentemente dalla corrente che lo attraversa. La figura 2.27 mostra il simbolo circuitale per un corto circuito ideale.
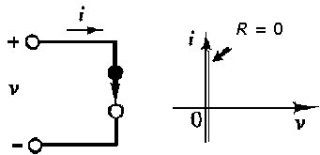
Figura 2.27 Corto circuito: R = 0, v = 0 per ogni i
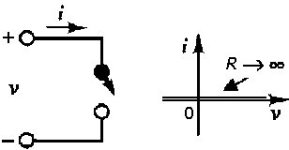
Figura 2.28 Circuito aperto: R → ∞, i = 0 per ogni v.
Fisicamente, ogni filo o altro conduttore metallico presenterà sempre una certa resistenza, per quanto piccola essa sia. A scopo pratico, tuttavia, sotto certe condizioni, molti elementi approssimano un corto circuito abbastanza accuratamente.
Un elemento circuitale la cui resistenza va all'infinito è chiamato circuito aperto. Intuitivamente, non ci si aspetta il passaggio di corrente attraverso un circuito aperto, giacché questo oppone una resistenza infinita ad ogni corrente. In un circuito aperto, ci si aspetta che la corrente sia nulla indipendentemente dalla tensione applicata dall'esterno. La figura 2.28 illustra questa idea.
Nella pratica non è molto difficile approssimare un circuito aperto: ogni interruzione di continuità nel conduttore di corrente funziona da circuito aperto.
Tuttavia, l'idealizzazione di circuito aperto, come definito in figura 2.28, non vale a tensioni molto alte. Infatti, la rigidità dielettrica del materiale, cioè la capacità di un materiale di impedire il passaggio di cariche, è un valore finito che varia da materiale a materiale.
Ad un valore sufficientemente alto di tensione (che dipenderà, a sua volta, dal materiale ovvero dalla sua rigidità dielettrica), il materiale non sarà più in grado di garantire l'isolamento tra i due morsetti in figura, e si genererà una scarica tra i morsetti stessi (principio, questo, sfruttato nei motori a combustione interna, dove l'isolante è dato dalla miscela carburante-aria). Il corto circuito ideale e il circuito ideale aperto sono concetti molto utili e trovano largo uso nell'analisi dei circuiti.
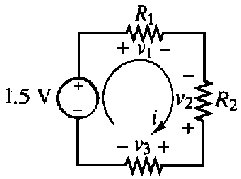
Per avere un esempio di circuito in serie, facciamo riferimento al circuito di figura 2.29, dove è stata collegata una pila ai resistori R1, R2 ed R3. Vale la seguente definizione:
Due o più elementi circuitali sono detti in serie se attraverso ciascuno di loro passa la stessa corrente.
 |
 |
| Figura 2.29 | |
Applicando la legge di Kirchhoff delle tensioni, si può verificare che la somma delle tensioni (differenze di potenziale) presenti ai capi dei tre resistori eguaglia la tensione fornita dall'esterno dalla pila:
1,5 = v1 + v2 + v3
e poiché, secondo la legge di Ohm, le singole tensioni possono essere espresse dalle relazioni:
v1 = iR1 v2 = iR2 v3 = iR3
possiamo scrivere, di conseguenza:
1,5 = i(R1 + R2 + R3)
Questo semplice risultato illustra un principio molto importante: per la pila, i tre resistori in serie appaiono come un unico resistore equivalente di resistenza REQ, dove:
REQ = (R1 + R2 + R3)
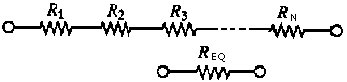
I tre resistori possono perciò essere sostituiti da un singolo resistore di resistenza REQ, senza cambiare la quantità di corrente richiesta alla batteria. Da questo risultato possiamo estrapolare la relazione più generale che definisce la resistenza equivalente di N resistori in serie:
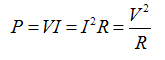 (F2.19)
(F2.19)
cioè: N resistori in serie sono equivalenti ad un singolo resistore di resistenza pari alla somma delle singole resistenze (figura 2.29).
Un concetto legato strettamente ai resistori in serie è quello del partitore di tensione. Questa terminologia nasce dall'osservazione che la tensione del generatore nel circuito di figura 2.29 si suddivide tra i tre resistori secondo la legge di Kirchhoff delle tensioni. Detta v0 la tensione del generatore di figura 2.29, pari a 1,5 V, se ora osserviamo che la corrente i è data da:
i = 1,5 / REQ = v0 / (R1 + R2 + R3)
possiamo scrivere ogni differenza di potenziale ai capi dei resistori così:
v1 = iR1 = v0(R1 / REQ) v2 = iR2 = v0(R2 / REQ) v3 = iR3 = v0(R3 / REQ)
il che ci porta a enunciare la seguente regola di partizione delle tensioni:
la tensione (differenza di potenziale) ai capi di ciascun resistore in un circuito in serie è direttamente proporzionale al rapporto tra la resistenza del resistore considerato e la resistenza totale equivalente del circuito in serie.
Un esercizio istruttivo consiste nel verificare che la legge di Kirchhoff delle tensioni è ancora soddisfatta, facendo la somma delle cadute di tensione lungo il circuito ed eguagliandola alla tensione del generatore:
v1 + v2 + v3 = v0(R1 / REQ) + v0(R2 / REQ) + v0(R3 / REQ) = v0
in quanto REQ = (R1 + R2 + R3). Pertanto, poiché la legge è soddisfatta, siamo certi che la regola di partizione delle tensioni è consistente con le leggi di Kirchhoff. In virtù della regola di partizione delle tensioni, possiamo sempre determinare la proporzione in cui sono distribuite nel circuito le cadute di tensione. Questo risultato sarà utile nel ridurre circuiti complicati a circuiti più semplici.
La forma generale della regola di partizione delle tensioni, per un circuito con N resistori in serie ed un generatore di tensione, è:
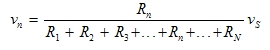 (F2.20)
(F2.20)
ove vn è la tensione ai capi del resistore n-esimo e vs è la tensione del generatore. La formula 2.20 è al cosidetta formula del partitore di tensione.
Determinare la tensione vX del resistore a sinistra nel circuito di figura 2.30.
Soluzione:
Se scegliamo la direzione di riferimento indicata in figura 2.30 quale direzione della corrente, possiamo assegnare la polarità delle tensioni nel circuito come raffigurato. Allora, applicando la legge di Kirchhoff delle tensioni, si ha:
3.0 - v10 - v6 - v8 = 0
ove v10 è la tensione ai capi del resistore da 10 Ω, in base alla direzione della corrente indicata in figura. Si noti che vX = v8. In base alla regola di partizione delle tensioni (formula 2.20), si ha:
vX = v8 = (8 / (8 + 6 + 10)) × (3) = 1 V

Figura 2.30
La tecnica impiegata in questo esempio è rappresentativa di come la regola di partizione delle tensioni si applica ai circuiti in serie. Il fattore chiave che deve essere determinato prima di applicare questa regola è se il circuito è nei fatti un circuito in serie.
Vedremo in futuro come sia possibile ridurre ad un circuito in serie circuiti più complessi.
Quando la corrente elettrica attraversa un filo metallico o un altro elemento circuitale, incontra una certa resistenza, la cui intensità dipende dalle proprietà elettriche del materiale. La resistenza al passaggio della corrente può essere indesiderata - per esempio nel caso di cavi per il trasporto della corrente - o può essere utilmente impiegata in un circuito elettrico. Nondimeno, praticamente tutti gli elementi circuitali presentano una certa resistenza; di conseguenza, il passaggio della corrente attraverso un elemento avrà come effetto la dissipazione di energia sotto forma di calore. Un resistore è un elemento circuitale a due terminali in cui tensione e corrente soddisfano la relazione:
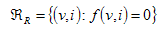 (F2.13)
(F2.13)
Questa relazione è detta caratteristica i-v del resistore, e può essere rappresentata graficamente sul piano i-v. Il resistore ideale è un dispositivo che mostra proprietà di resistenza lineari in accordo alla legge di Ohm, che afferma che:
V = RI (F2.14)
cioè, la tensione attraverso un elemento è direttamente proporzionale alla corrente che lo attraversa, e la costante di proporzionalità è data dalla resistenza R. In tal modo, il grafico della caratteristica di un resistore ideale è una linea retta passante sempre per l'origine degli assi del piano i-v. L'unità di misura della resistenza è l'ohm, che per la (2.14) risulta essere:
1 Ω = 1 V/A
La resistenza di un materiale dipende da una proprietà chiamata resistività, che viene indicata con il simbolo ρ; il reciproco della resistività è chiamato conduttività e viene indicato con il simbolo σ. Per un elemento di resistenza cilindrico (mostrato in figura 2.21), la resistenza è proporzionale alla lunghezza del campione, l, ed inversamente proporzionale alla sua sezione trasversale, A, e conduttività, σ:
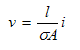 (F2.15)
(F2.15)
E' spesso conveniente definire la conduttanza di un elemento circuitale come il reciproco della sua resistenza. Il simbolo della conduttanza di un elemento è la G, dove:
G = 1 / R siemens (S) dove 1 S = 1 A/V = 1 Ω-1 (F2.16)
Perciò, la legge di Ohm può essere riscritta in termini di conduttanza:
I = GV (F2.17)
e sarà perciò: f(v,i) = v × Ri ovvero f(v,i) = i × Gv (N.B.: v e i possono essere funzioni del tempo: in ogni caso, la linearità prevede che v(t) = Ri(t) ovvero i(t) = Gv(t) ).
Occorre fare attenzione a non confondere i termini resistenza e resistore: la resistenza è la proprietà del materiale di opporsi al passaggio della corrente, il resistore è l'oggetto fisico che rappresenta il modello teorico. Per ogni materiale, il valore della resistività ρ dipende infatti dalla temperatura T secondo la legge:
ρ = ρ0(1 + α(T)) × ΔT
ove α(T) è un coefficiente (detto coefficiente di temperatura) funzione della temperatura (in generale), la cui unità di misura è ppm/Kelvin o ppm/Celsius (ppm = parti per milione = 10-6 ; è un numero puro), mentre ρ0 è la resistività allo 0° K o C. Nell'intorno della temperatura ambiente, e per ΔT non troppo elevati, si può assumere α costante.
La legge di Ohm è una relazione empirica che trova larghissima applicazione in elettrotecnica, a causa della sua semplicità. E', tuttavia, solo un'approssimazione della fisica dei materiali conduttori di elettricità. Tipicamente, la relazione lineare tra tensione e corrente nei conduttori elettrici non vale per alti valori di tensione e corrente. Inoltre, non tutti i materiali conduttori di elettricità mostrano un comportamento lineare anche per piccole tensioni e correnti.
Tuttavia, è di solito vero che per un certo campo di tensioni e correnti, moltissimi elementi mostrano una caratteristica i-v lineare. La figura 2.20 illustra come il concetto di resistenza lineare si può applicare agli elementi con caratteristica i-v non lineare, definendo graficamente la porzione lineare della caratteristica i-v per due comuni dispositivi elettrici: la lampadina, già incontrata in precedenza, ed il diodo semiconduttore.
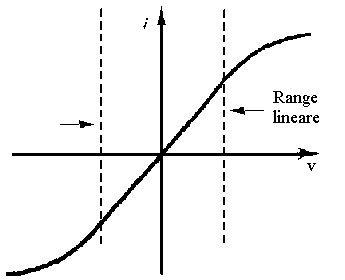 Lampadina |
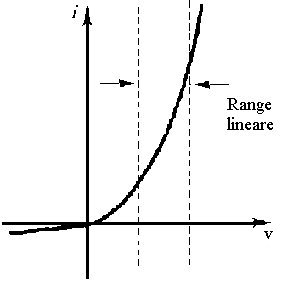 Diodo semiconduttore (caratteristica esponenziale) |
| Figura 2.20 Caratteristiche reali di due carichi | |
La forma tipica ed il simbolo circuitale del resistore sono mostrati in figura 2.21. Resistori fatti di sezioni cilindriche di carbonio (con resistività ρ = 3.5 × 10-5 Ω m) sono molto comuni e sono commercialmente disponibili per un ampio campo di valori di resistenza e di potenza tollerata. Un'altra tecnica di produzione comunemente impiegata per i resistori impiega un film metallico. Nei circuiti elettronici (ad esempio nelle radio e nei televisori) è comune l'uso di resistori con potenza tollerata pari ad 1/4 W.
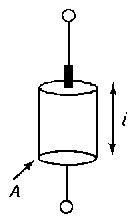 Rappresentazione fisica del resistore |
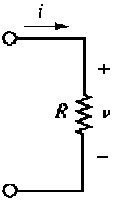 Rappresentazione simbolica del resistore |
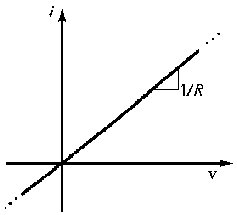 Caratteristica i-v del resistore |
|
| Figura 2.21 Rappresentazione fisica, simbolica e caratteristica di un resistore | |
Per sapere la resistenza in ohm offerta dal resistore, si usa una convenzione a bande colorate, in cui ad ogni colore corrisponde un valore da 1 a 10; sul resistore vengono dipinte 4 bande: tre servono per il calcolo della resistenza (b1 ,b2 ,b3), la quarta, b4, serve per sapere la percentuale di tolleranza.
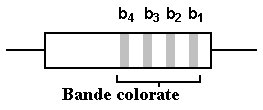 Figura 2.22 Codice a colori del resistore
Figura 2.22 Codice a colori del resistore
|
Colore
|
Significato |
Colore
|
Significato |
|
Nero
|
0 |
Blu
|
6 |
|
Marrone
|
1 |
Viola
|
7 |
|
Rosso
|
2 |
Grigio
|
8 |
|
Arancio
|
3 |
Bianco
|
9 |
|
Giallo
|
4 |
Argento
|
10% |
|
Verde
|
5 |
Oro
|
5% |
La formula per calcolare R è data costruendo il numero a partire dalle bande b1 (decina) e b2 (unità): questo va moltiplicato per 10 elevato al valore dato dalla banda b3:
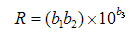 (F2.18)
(F2.18)
Per esempio, se le prime tre bande colorate sul resistore sono rosso (b1 = 2), violetto (b2 = 7) e giallo (b3 = 4), il valore della resistenza è R = 27 × 104 = 270000 Ω = 270 kΩ.
In aggiunta alla resistenza in ohm, per i resistori commerciali viene solitamente specificata la massima dissipazione di potenza consentita, ovvero la massima potenza tollerata (power rating = letteralmente "tasso di potenza"). Se si supera la potenza tollerata, si ha surriscaldamento ed il resistore può letteralmente prendere fuoco. Per un resistore R, la potenza dissipata è data dalla legge di Joule:
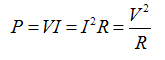 (F2.19)
(F2.19)
cioè, la potenza dissipata da un resistore è proporzionale al quadrato della corrente che lo attraversa, come anche al quadrato della differenza di potenziale ai sui estremi.
Una tipica potenza massima tollerata per un resistore al carbonio impiegato in circuiti elettronici a bassa potenza è 1/4 W. Qual è il valore di resistenza che deve avere il più piccolo resistore a 1/4 W per poterlo collegare ad una pila da 1,5 V (figura 2.23)?
Soluzione:
Per ricavare la resistenza R, calcoliamo prima la potenza dissipata dal resistore come funzione della sua resistenza. Dalla legge di Joule si ha:
P = VI = V(V/R) = V2/R = 1,52/R
Poiché la massima potenza tollerabile è 1/4 W, possiamo scrivere:
P = 0,25 = 2,25/R da cui: R = 2,25 / 0,25 = 9 Ω
Pertanto R deve essere almeno di 9 Ω.
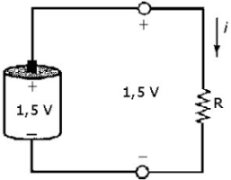 |
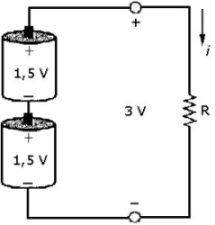 |
| Figura 2.23 | Figura 2.24 |
Come cambierebbe questo risultato se la tensione venisse raddoppiata? Con facili conti si trova che la potenza dissipata è ora data da P = 32/R, e che perciò R deve essere almeno di 36 Ω per non superare la massima potenza tollerata. Questo risultato è mostrato in figura 2.24. Si noti l'effetto della relazione quadratica: raddoppiando la corrente, R aumenta di un fattore pari a 4.
Il principio illustrato in questo esempio è alla base di molti trasduttori a spostamento in commercio. Il resistore in figura 2.25 è un resistore a serpentina filiforme - cioè, è un resistore fatto di un sottile filo a spira elicoidale molto stretta - che presenta una resistenza di 0.1 Ω per spira.
Il puntatore collegato al carrello mobile fa contatto con il resistore, chiudendo, così, il circuito a distanza x dall'origine. Ogni spira occupa 0,5 mm, a la lunghezza totale L del resistore è 10 cm. Trovare la tensione in uscita V0 in funzione dello spostamento del carrello, x.
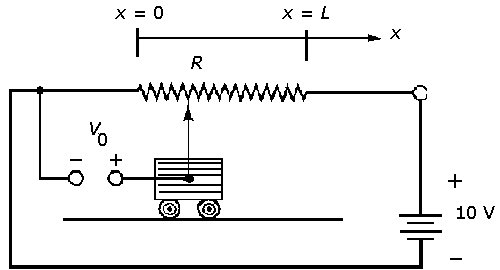
Figura 2.25 Trasduttore resistivo a spostamento
Soluzione:
Il numero totale di spire nel resistore è dato dalla seguente espressione:
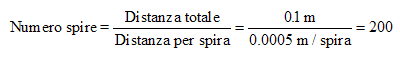
Ciò significa che la resistenza totale da 0 a L è pari a 20 Ω. Pertanto, possiamo determinare la relazione tra la posizione del carrello e la resistenza tra l'origine ed il punto x come segue:
R(x) = (20/10)x = 2x Ω
dove x è la distanza misurata in centimetri. La tensione in uscita può essere trovata considerando la legge di Ohm (2.14):
I = 10 V/ 20 Ω = 0,5 A da cui V0 = IR(x) = (0,5)2x = x
Così, la posizione relativa del carrello mobile, in centimetri, è numericamente uguale alla tensione V0.
Gli strain gauges sono dispositivi che vengono attaccati sulla superficie di un oggetto, ad esempio un provino, e la cui resistenza varia in funzione della deformazione cui va soggetto il provino dopo l'applicazione dello strain gauge. Gli strain gauges possono essere usati per misure di deformazione, sforzo, torsione e compressione. Si è visto che la resistenza di un conduttore cilindrico di sezione trasversale A, lunghezza L e conduttività σ è data dall'espressione:
R = L / (σA)
Se il conduttore è compresso o allungato come conseguenza dell'applicazione di una forza esterna, cambieranno le sue dimensioni, e con esse la resistenza. In particolare, se il conduttore è teso, diminuirà la sua sezione trasversale ed aumenterà la resistenza. Se il conduttore è invece compresso, la sua resistenza diminuisce, in quanto diminuirà la lunghezza L. La relazione tra variazione di resistenza e variazione di lunghezza è data dal fattore di Gauge G definito da:
G = (ΔR / R) / (ΔL / L)
e poiché la deformazione ε è definita dalla formula ε = ΔL/L, la variazione di resistenza a seguito di una deformazione applicata ε è data dall'espressione:
ΔR = R0Gε
dove R0 è la resistenza dello strain gauge in assenza di deformazione, ed è detta resistenza a deformazione zero.
 a) |
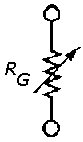 b) |
| Figura 2.25 Strain gauge a resistenza: a) simbolo fisico, b) simbolo circuitale | |
Il valore di G per strain gauges costituiti da una lamina di metallo è usualmente 2. La figura 2.26a mostra un tipico strain gauge in lamina di metallo. La lamina è ottenuta mediante un processo di fotoincisione ed il suo spessore è inferiore a 0,00002 m.
Valori tipici di resistenza sono 120, 350 a 1000 Ω. Le aree più ampie sono delle piazzole (pads in inglese) per la connessione elettrica. La deformazione massima che può essere misurata da uno strain gauge a lamina va da circa lo 0.4 allo 0.5%: cioè si ha un rapporto ΔL/L= 0.004-0.005. Per uno strain gauge a 120 Ω, ciò corrisponde ad una variazione di resistenza dell'ordine dei 0.96 fino a 1.2 Ω.
Benché questa variazione di resistenza sia molto piccola, essa può essere misurata tramite un'opportuna circuiteria. Esistono anche strain gauges a cristalli di silicio opportunamente drogati. Gli strain gauges a resistenza sono solitamente connessi ad un circuito chiamato ponte di Wheatstone, che vedremo in seguito.
La relazione tra corrente e tensione ai morsetti di un elemento circuitale definisce il comportamento di quell'elemento nel circuito. Introdurremo ora un mezzo grafico di rappresentazione delle caratteristiche (ai morsetti) degli elementi circuitali.
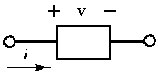
Figura 2.17 Rappresentazione generale di elemento circuitale
La figura 2.17 mostra l'immagine che sarà impiegata quale simbolo di un generico elemento circuitale: la variabile i rappresenta la corrente che passa attraverso l'elemento, mentre v è la differenza di potenziale, o tensione, agli estremi dell'elemento.
Supponiamo ora che agli estremi dell'elemento circuitale venga imposta una tensione nota. La corrente che dovrebbe fluire come conseguenza di questa tensione, e la tensione stessa, formano un'unica coppia di valori. Se si variasse la tensione applicata all'elemento e si misurasse la corrente che ne risulta, sarebbe possibile costruire una relazione funzionale tra corrente e tensione, relazione nota come caratteristica i-v (o caratteristica volt-ampère). tale relazione definisce l'elemento circuitale, nel senso che se noi imponiamo una tensione (o corrente) predeterminata, la corrente (o tensione) risultante è ricavabile in modo diretto dalla caratteristica i-v. Una diretta conseguenza di ciò è che la potenza dissipata, o generata, dall'elemento può a sua volta essere determinata dalla curva i-v.
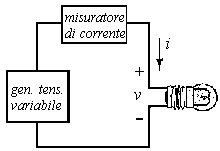
La figura 2.18 mostra un esperimento per la determinazione empirica della caratteristica i-v di una lampadina a filamento di tungsteno. Un generatore variabile di tensione viene impiegato per applicare varie tensioni, e per ogni tensione applicata viene misurata la corrente che passa attraverso l'elemento.
 |
|
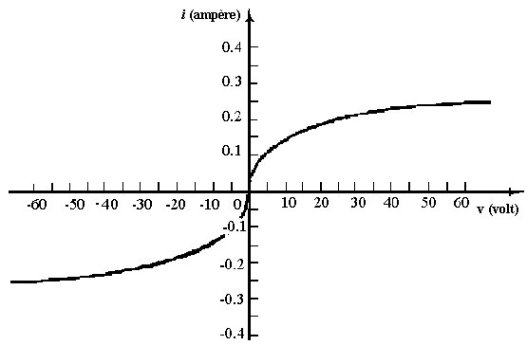
| Figura 2.18 caratteristica volt-ampere di una lampadina a filamento di tungsteno | |
Potremmo certamente esprimere la caratteristica i-v di un elemento circuitale in forma funzionale:
In talune circostanze, tuttavia, è preferibile la rappresentazione grafica, specie quando la relazione tra corrente e tensione non è semplice. La forma più semplice della caratteristica i-v per un elemento circuitale è quella lineare, cioè:
ove k è una costante. Vedremo tra poco come questo semplice modello di un elemento circuitale sia abbastanza utile nella pratica e come possa essere usato per definire i più comuni elementi circuitali: i generatori di tensione e corrente ideali, ed il resistore.
Possiamo anche correlare la rappresentazione grafica i-v degli elementi circuitali alla potenza dissipata o generata da un elemento circuitale. Per esempio, la rappresentazione grafica della caratteristica i-v della lampadina di figura 2.18 mostra che quando la lampadina è attraversata da una corrente positiva, la tensione è positiva, e che, viceversa, un flusso di corrente negativa corrisponde ad una tensione negativa. In entrambi i casi, la potenza dissipata dal dispositivo è una quantità positiva, come deve, in base alla discussione fatta nella lezione precedente, giacché la lampadina è un dispositivo passivo.
Si noti ora che la caratteristica i-v compare in solo due dei quattro possibili quadranti nel piano i-v. Negli altri due quadranti, il prodotto tra tensione e corrente (cioè la potenza) è negativo, ed una curva i-v in entrambi questi quadranti corrisponderebbe, perciò, a potenza generata.
Ciò non è possibile per un carico passivo quale la lampadina; tuttavia, ci sono dispositivi elettronici che sono in grado di operare, per esempio, in tre dei quattro quadranti della caratteristica i-v e possono pertanto comportarsi come generatori di energia per particolari combinazioni di tensione e corrente. Ad esempio, un fotodiodo può agire sia in modo passivo (come sensore ottico) sia in modo attivo (come cella solare).
La caratteristica i-v dei generatori ideali di corrente e tensione può anche essere utile nel rappresentare visualmente il loro comportamento. Un generatore ideale di tensione produce una predeterminata tensione indipendentemente dalla corrente richiesta dal carico; di conseguenza, la caratteristica i-v risulta essere una linea diritta verticale la cui intercetta con l'asse delle ascisse (asse delle tensioni) corrisponde alla tensione del generatore.
Analogamente, la caratteristica i-v di un generatore ideale di corrente è una linea orizzontale la cui intercetta con l'asse delle ordinate (asse delle correnti) corrisponde alla corrente del generatore. La figura 2.19 illustra questo comportamento.

A) Caratteristica i-v di un generatore ideale di tensione di 4 V
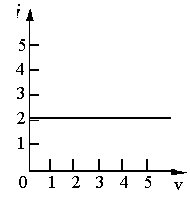
B) Caratteristica i-v di un generatore ideale di corrente di 2 A
Figura 2.19 Caratteristica i-v di generatori ideali
La definizione di tensione come lavoro per unità di carica si presta per se stessa all'introduzione del concetto di potenza. La potenza è definita come lavoro compiuto nell'unità di tempo. Perciò la potenza P, sia essa generata oppure dissipata da un elemento circuitale, può essere rappresentata dalla seguente relazione:
 (F2.9)
(F2.9)
Pertanto, la potenza elettrica generata da un elemento attivo, o dissipata o accumulata da un elemento passivo, è uguale al prodotto della tensione (differenza di potenziale) presente ai capi dell'elemento, per la corrente che lo attraversa. In forma analitica:
P = VI (F2.10)
E' facile verificare che l'unità di misura della tensione (joule/coulomb) moltiplicata per quella della corrente (coulomb/secondo) dà proprio l'unità di misura della potenza (joule/secondo = watt)
E' importante comprendere che, così come la tensione, la potenza è una quantità con segno, e che è necessario fare una distinzione tra potenza positiva e negativa. Questa distinzione può essere compresa facendo riferimento alla figura 2.11, in cui sono mostrati un generatore ed un carico.
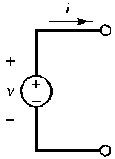 Potenza dissipata = v(-i) = (-v)i = -vi Potenza generata = vi |
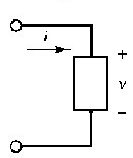 Potenza dissipata = vi Potenza generata = v(-i) = (-v)i = -vi |
| Figura 2.11 Convenzione di segno per un generatore ed un carico | |
La polarità della tensione ai morsetti del generatore e la direzione della corrente indicano che il generatore di tensione compie lavoro nel muovere la carica da un potenziale più basso ad un potenziale più alto. D'altra parte, il carico dissipa energia, dal momento che la direzione della corrente mostra che la carica è trasferita da un potenziale più alto ad un potenziale più basso. Per evitare confusione sul segno della potenza, si adotta la convenzione di considerare positiva la potenza dissipata dal carico (ovvero la potenza prodotta dal generatore). In altro modo si può esprimere lo stesso concetto dicendo che se la corrente fluisce da un potenziale più alto ad uno più basso (cioè da + a * ), la potenza dissipata sarà una quantità positiva.
Consideriamo, a titolo di esempio, il circuito in figura 2.12: un generatore indipendente di tensione vs agisce da ingresso sul resistore R1; il generatore comandato di corrente (CCCS) genera, invece, una corrente βi1 , cioè una corrente proporzionale alla corrente i1. Vogliamo determinare la tensione d'uscita v0 ai capi del secondo resistore lineare R2 ed il guadagno di potenza. Sappiamo che al nodo tra i due generatori ed il carico si ha, per la legge di Kirchhoff delle correnti:
dal momento che i2 = βi1. Ai capi della resistenza R1 si ha:
mentre ai capi della resistenza R2 si ha:
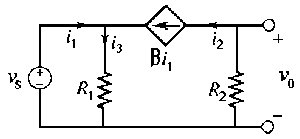 |
| Figura 2.12 |
La potenza fornita dal generatore esterno al circuito è quindi data dalla seguente formula:
p1 = v1i1 = R1(1 + β)i12
La potenza fornita dal circuito al resistore di carico R1 è:
p0 = v0(-i2) = -R2β2i12
Quindi, il guadagno di potenza è:
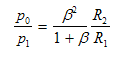
Fissato β, si può ottenere il guadagno voluto scegliendo opportunamente i valori di R1 e R2.
E' importante anche notare che gli effettivi valori numerici delle tensioni e delle correnti non importano: una volta che si è stabilita un'appropriata direzione di riferimento e si è applicata la convenzione sopra esposta in maniera consistente, la soluzione sarà corretta indipendentemente dalla direzione di riferimento scelta. Gli esempi che seguono illustrano questo fatto.
Vogliamo vedere che qualsiasi sia la direzione di riferimento, la soluzione è la stessa, purché sia applicata consistentemente la convenzione di segno. Il circuito di figura 2.13 consiste in un generatore (la batteria) con due carichi collegati in serie. Assumiamo dapprima arbitrariamente la direzione oraria come direzione della corrente. Calcoliamo la potenza dissipata da ciascun elemento. Poiché la corrente passa dal morsetto negativo a quello positivo nella batteria, la potenza dissipata dalla batteria sarà:
PB = (-vB)(i) = (-12)(0.1) = -12 W
Come si vede, la batteria genera 1.2 W. Secondo la stessa convenzione, i due carichi dissiperanno potenza secondo le relazioni:
P1 = (v1)(i) = (8)(0.1) = 8 W
P2 = (v2)(i) = (4)(0.1) = 4 W
Pertanto, l'energia si conserva, poiché la potenza netta dissipata nel circuito è zero.
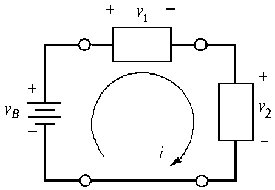 vB = 12 V v1 = 8 V i = 0.1 A v2 = 4 V |
| Figura 2.13 |
Consideriamo ora lo stesso circuito, ma assumiamo ora come verso arbitrario della corrente quello antiorario, come mostrato in figura 2.14. Le tensioni risultanti dalla direzione assunta per la corrente sono mostrate in figura.
Si noti che, per conservare la convenzione di segno, i segni delle tensioni sono opposti rispetto a quelli di figura 2.14: la tensione della batteria è ora -12 V, e le tensioni alle estremità dei carichi sono, rispettivamente, -8 V e -4 V. Di conseguenza, in base alla convenzione di segno, la potenza dissipata dalla batteria è:
PB = (-vB)(i)= -(-12)(-0.1) = -12 W
mentre la potenza dissipata dai carichi è:
P1 = (v1)(i) = (-8)(-0.1) = 8 W
P2 = (v2)(i) = (-4)(-0.1) = 4 W
Come nel caso precedente, la convenzione di segno ci dice che la batteria genera 1.2 W di potenza, che viene dissipata dai due carichi.
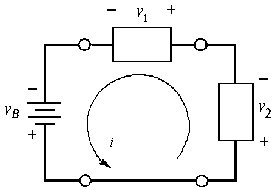
vB = -12 V v1 = -8 V i = -0.1 A v2 = -4 V
Figura 2.14
Questo esempio illustra come possiamo determinare se un elemento sconosciuto è un generatore o un carico, semplicemente identificando le polarità delle tensioni e le direzioni della corrente. Assumiamo che siano disponibili dei dispositivi che ci consentono di misurare tensioni e correnti nel circuito sconosciuto di figura 2.15. Osservando la figura, determinare quale elemento fornisce energia e quale invece la dissipa.

Figura 2.15
Soluzione:
Osservando l'elemento circuitale B, ci rendiamo conto che questo agisce da generatore, poiché la corrente passa da un punto a più basso potenziale ad un punto a più alto potenziale, come si vede in figura 2.16. Pertanto, la potenza dissipata dall'elemento B è:
PB = (vB)(i) = (100)(-20) = -2000 W = -2 kW
Questo significa che l'elemento B fornisce 2 kW di potenza all'elemento A, che funge, perciò, da carico.
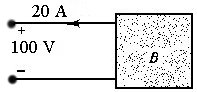
Figura 2.16
Negli esempi precedenti, si è utilizzata una pila come generatore di corrente, nell'ipotesi implicita che la tensione da essa fornita (ad esempio, 1.5 Volts per una pila alcalina, 12 Volts per una batteria acido-piombo d'auto) sia fissata. Con tale assunzione, implicitamente trattiamo la pila come un generatore ideale. Andremo ora a definire i generatori ideali. Intuitivamente, un generatore ideale è quello che fornisce una arbitraria quantità di energia.
I generatori ideali sono divisi in due tipi: generatori di tensione e generatori di corrente. Di questi due tipi, si è probabilmente più familiari con il primo, giacché pile (a secco o alcaline) e batterie acido-piombo sono tutte generatori di tensione (e non sono, naturalmente, ideali).
E' difficile pensare ad un esempio fisico che approssimi il comportamento di un generatore ideale di corrente; tuttavia, esistono anche delle approssimazioni ragionevolmente buone di un generatore ideale. Ad esempio, un generatore di tensione collegato in serie con un elemento circuitale che oppone una grande resistenza al flusso di corrente, fornisce una corrente pressoché costante, benché piccola, e pertanto si comporta come se di fatto fosse un generatore ideale di corrente.
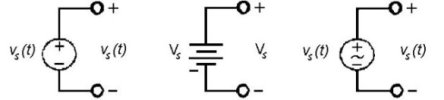
Un generatore di tensione ideale è un dispositivo elettrico che genera una tensione predeterminata ai suoi morsetti. La capacità di un generatore ideale di tensione di fornire la sua tensione in uscita non è influenzata dalla corrente che esso deve fornire agli altri elementi circuitali. In altre parole:
Un generatore ideale di tensione fornisce una prescritta tensione ai suoi morsetti indipendentemente dalla corrente che lo attraversa. La quantità di corrente fornita dal generatore è determinata dal circuito ad esso collegato.
 |
||
| a) | b) | c) |
| Figura 2.7 Generatori ideali di tensione | ||
La figura 2.7 mostra i vari simboli per i generatori di tensione che saranno usati in seguito. Il simbolo di tipo a) è quello generale; in generale, la tensione in uscita da un generatore ideale vs(t) può essere funzione del tempo, ma può anche essere costante (in inglese indicata con la sigla DC = direct current). Il simbolo b) è invece usato nel solo caso specifico di generatori di tensione costante (è la batteria ideale). Infine, il simbolo c) è impiegato nel caso specifico di generatori di tensione sinusoidale (ad esempio: vs(t) = V cos(ωt).
In generale, salvo diversa segnalazione, sarà usata la seguente notazione: un generico generatore di tensione sarà indicato con la lettera minuscola v. Se è necessario enfatizzare che il generatore produce una tensione che varia nel tempo, allora si userà la notazione v(t). Infine, un generatore di tensione costante (DC) sarà indicato con la lettera maiuscola V. Si noti che per convenzione il verso positivo della corrente è quello uscente dal morsetto positivo del generatore.
 |
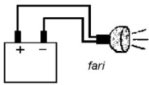 |
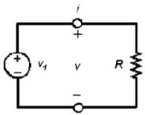
| a) rappresentazione simbolica | b) rappresentazione fisica |
| Figura 2.8 Varie rappresentazioni di un sistema elettrico | |
Consideriamo la figura 2.8: essa rappresenta il collegamento tra un generatore di energia e un circuito passivo (cioè un circuito che può assorbire e dissipare energia - per esempio, i fari e le lampadine degli esempi precedenti). Sono mostrate due rappresentazioni diverse: simbolica e fisica; nell'analisi dei circuiti elettrici, noi scegliamo di rappresentare la realtà fisica di figura 2.8(b) tramite l'approssimazione fornita dagli elementi circuitali ideali, come raffigurato in figura 2.8(a).
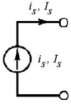
Un generatore ideale di corrente è un dispositivo che è in grado di generare una corrente costante indipendentemente dal circuito a cui è collegato. A tal fine, esso deve essere in grado di generare una tensione arbitraria ai suoi morsetti. La figura 2.11 mostra il simbolo usato per rappresentare il generatore ideale di corrente. Per analogia con la definizione di generatore ideale di tensione, possiamo scrivere:
Un generatore ideale di corrente fornisce una predeterminata corrente a qualsiasi circuito esso venga collegato. La tensione generata dal generatore è determinata dal circuito cui esso è collegato.
La stessa convenzione vista per i generatori di tensione viene usata per i generatori di corrente: si userà la lettera minuscola i per indicare un generico generatore di corrente, e la lettera maiuscola I per indicare un generatore di corrente continua.
I generatori finora descritti sono in grado di generare una predeterminata tensione o corrente indipendentemente da ogni altro elemento all'interno del circuito. Vengono perciò detti generatori indipendenti. Esiste, tuttavia, un'altra categoria di generatori, il cui output (corrente o tensione) è funzione di qualche altra tensione o corrente in un circuito: vengono perciò chiamati generatori dipendenti (o controllati o comandati).

Figura 2.10 Simboli per i generatori dipendenti
Per rappresentare tali generatori (e distinguerli da quelli indipendenti) si usa un simbolo diverso, a forma di rombo. I simboli tipicamente usati sono quelli di figura 2.10; la tabella seguente illustra le relazioni tra tensione o corrente del generatore e la tensione o corrente da cui esso dipende - vx o ix, rispettivamente - che possono essere qualsiasi tensione o corrente nel circuito.
| Tipo di generatore | Relazione |
| Generatore di tensione a tensione controllata (VCVS = voltage controlled voltage source) |
vs = A vx |
| Generatore di tensione a corrente controllata (CCVS = current controlled voltage source) |
vs = A ix |
| Generatore di corrente a tensione controllata (VCCS = voltage controlled current source) |
is = A vx |
| Generatore di corrente a corrente controllata (CCCS = current controlled current source) |
is = A ix |